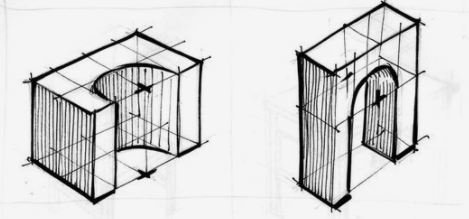
Las perspectivas son muy importantes en áreas como arquitectura o en asignaturas como dibujo técnico. Uno de los tipos más utilizados es la Perspectiva Isométrica. En este artículo te explicamos en qué consiste, qué aplicaciones tiene y cómo elaborarla. Quédate y descúbrelo.
¿Qué es la Perspectiva Isométrica?
La Perspectiva Isométrica es un sistema de representación gráfica, también llamado axonométrica cilíndrica ortogonal. Este sistema se basa en la representación visual en dos dimensiones de un objeto tridimensional, en cuya representación los tres ejes ortogonales principales forman ángulos de 120º y las dimensiones paralelas a estos ejes se suelen medir en una misma escala.
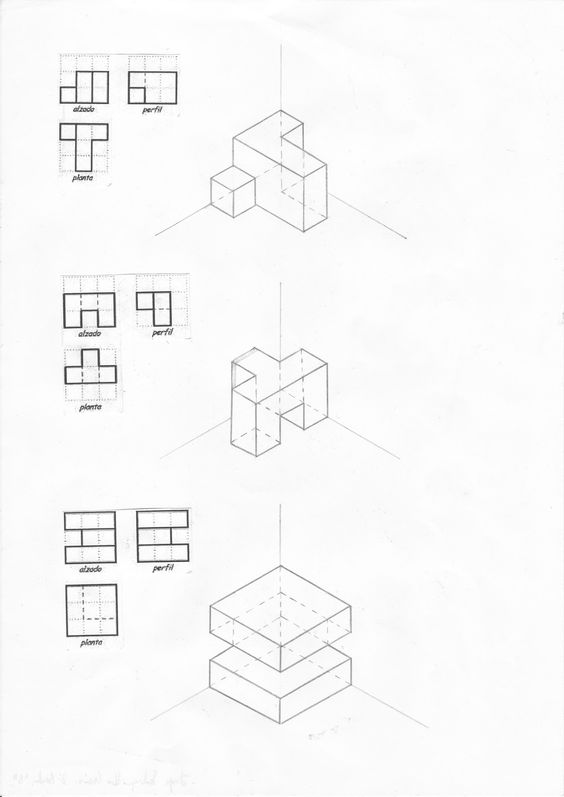
La isometría puede definirse como una forma de proyección empleada sobre todo para dibujo técnico cuya ventaja es que permite la representación a escala, y su desventaja es que no refleja la disminución aparente de tamaño en proporción a la distancia percibida por el ojo humano.
¿Quieres saber más acerca de este tipo de perspectiva y cómo realizarla? Entonces sigue leyendo.
Esta perspectiva puede visualizarse considerando la vista de una habitación cúbica desde un vértice superior mirando hacia el opuesto. El eje x es la diagonal hacia la derecha y hacia abajo, el eje y es la diagonal hacia la izquierda y hacia abajo, y el eje z permanece vertical. La profundidad se muestra a través de la altura de la imagen. Las líneas paralelas a los ejes divergen 120º unas de las otras.
La isometría determina una dirección de visualización en la cual la proyección de los ejes coordenados x, y, z forman el mismo ángulo, es decir, 120° entre sí. Los objetos se suelen mostrar con una rotación del punto de vista de 30º en las tres direcciones principales.
La principal característica de este tipo de perspectiva es que los ejes visuales son paralelos entre sí. Debido a esto, se sitúa en el infinito el punto de vista de la proyección. La ventaja que posee representar objetos de esta forma, es que es posible medir directamente los tres ejes de coordenadas para saber las dimensiones reales del objeto que se representa. Por ello, en la perspectiva isométrica los tres ángulos que forman parte de los ejes de coordenadas son iguales, cada uno tiene 120º de ángulo. Esto permite obtener las medidas del objeto sin tener que proceder a escalarlas entre sí.
La perspectiva isométrica normalmente utiliza un coeficiente de reducción para las dimensiones equivalente a 0.82. También es necesario comentar que existe el dibujo isométrico donde no se utiliza coeficiente de reducción sino la escala 1:1 o escala natural.
¿Cómo se dibuja una pieza en Perspectiva Isométrica?
Para dibujar un objeto con la perspectiva isométrica, tiene que seguir los siguientes pasos:
Dibujar el volumen envolvente
- Dibujar los ejes
Para dibujar los ejes debes colocar la escuadra abajo como soporte con la hipotenusa horizontal. Esta regla es la que debes sujetar firmemente con la mano con la que no dibujas, de este modo tendrás tu mano dominante libre para dibujar.
El cartabón se debe desplazar sobre la escuadra suavemente y, cuando lo tengas en la posición adecuada, lo sujetas con un dedo de la mano izquierda, mientras mantienes todavía muy fija la escuadra.

- Decidir la posición de la pieza
La pieza suele venir dada por 3 vistas: planta, alzado y perfil. Debido a que trabajamos con el sistema europeo, si el perfil nos lo dan situado a la derecha se trata del perfil lateral izquierdo, y viceversa.
Las proyecciones utilizadas en el sistema europeo son consideradas sobre unos planos ortogonales entre sí, situados normalmente detrás de la pieza. Al desplegar estos 3 planos para transformarlos en plano de dibujo, el perfil izquierdo se queda en las vistas a la derecha.
De la misma forma, el alzado que se ve en la perspectiva en la derecha aparece en las vistas en la izquierda. Para finalizar, la planta que es la vista superior de la perspectiva se ve en las vistas justo debajo del alzado.
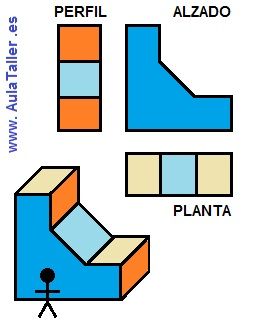
- Tomar las medidas para cada eje
Si se da el caso de que las vistas de la pieza no sean rectángulos o cuadrados completos, tendrás que dibujar dichos rectángulos. En segundo lugar, debes tomar las medidas y llevarlas a cada eje:
- El ancho del alzado debe ir del eje perpendicular a la dirección que hemos marcado anteriormente como alzado.
- El ancho del perfil irá del eje perpendicular a la vista del perfil.
- La altura del alzado irá al eje vertical.
Si tomas dichas medidas y los llevas a los ejes correspondientes, obtienes los puntos 1, 2 y 3.
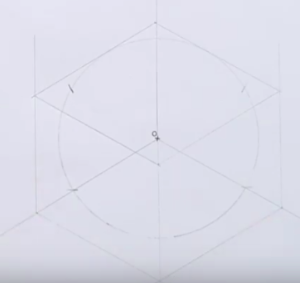
- Dibujar paralelas a los ejes hasta conseguir cerrar el paralelogramo
Si dibujas una recta paralela al eje Y por el punto 3 y otra paralela al eje Z por el punto 1, obtendrás el punto 4. Después, debes dibujar una paralela a X por 1 y otra paralela a Y por 2, y obtendrás el punto 5. Y por último, con una paralela a X por el punto 3 y otra paralela a Z por el punto 2, encontrarás el punto 6.
Con estas rectas obtienes las paredes del fondo. Para cerrar el cubo sólo falta dibujar una paralela a X por el punto 4, una paralela a Y por el punto 6 y una paralela a Z por el punto 5.
Y con eso tienes el vértice 7 que cierra el paralelogramo.
Dibujar las vistas sobre las caras de la pieza
- Dibujar la planta
La planta es lo que se considera la vista desde arriba y esta se dibuja en la cara 3-4-7-6. La recta horizontal que corta por la mitad la planta es una recta paralela al eje Y que pasa por el punto medio de la arista 4-7. La recta oblicua va desde ese mismo punto de la arista 4-7 al punto medio de la arista 6-7 el cual podemos obtener tomando la referencia del alzado. Posteriormente se dibuja una recta vertical desde el punto medio del alzado.
- Dibujar el perfil
El perfil es el derecho y por ello se tiene que dibujar sobre la cara 1-4-7-5. La división en vertical de 1,5 cm no es necesario repetirla, debido a que esta coincide con la división que ya se ha hecho previamente para el alzado. Por lo tanto, se debe trazar una paralela al eje X por ese punto medio de la arista 5-7.
La división en horizontal, también de 1,5 cm se lleva a la arista 1-5 y después en vertical hasta que corta a la recta trazada anteriormente. Únelo con el vértice 5 y dibuja una recta vertical.
- Dibujar el alzado sobre la perspectiva
El alzado se debe situar a la derecha, teniendo eso en cuenta dibujaremos sobre la cara 2-5-7-6. Toma la medida divisoria en altura y llévala a la arista 2-6 de la perspectiva. Desde ahí dibuja una paralela al eje Y.
La división en anchura del alzado debes llevarla a la arista 2-5. Debido a que el punto que nos interesa está sobre la recta que hemos dibujado previamente, dibuja una recta vertical desde el punto medio de la arista hasta la recta trazada. Este punto hay que unirlo con el vértice 5.
Quitar los bocados evidentes
En el caso de que el contorno de algunas de las vistas no sea un rectángulo, se puede eliminar completamente este bocado de la perspectiva. En un paso estás eliminando volumen sobrante y estás moldeando la pieza con la seguridad de que lo estás haciendo correctamente. Este método funciona de la misma forma en planta, alzado y perfil, por lo que su efecto se suma.
Encontrar relaciones en las vistas y proyecta hacia el fondo
El ejemplo más sencillo para poder explicar este paso es el de un punto A en un paralelogramo. Empezamos con el paralelogramo completo ya dibujado en la perspectiva y la ubicación de las proyecciones del punto en planta a, alzado a’ y perfil a’’.
La planta está dibujada sobre el plano XY, entonces la perpendicular es el eje Z. Se dibuja una recta paralela al eje Z por la proyección a. Se procede ahora con el punto a’ del alzado. El alzado está dibujado en el plano YZ y una perpendicular sería el eje X. La intersección de las dos rectas que se acaba de dibujar definiría la posición real del punto A.
A modo de comprobación se puede proyectar también la vista a’’ del punto en el perfil, en una recta paralela al eje Y. Observa que las 3 líneas se cortan en un único punto, el punto A.
Busca superficies completas
Cada superficie está limitada por vértices y aristas, que son las que debemos encontrar en la perspectiva. Se pueden encontrar superficies planas o superficies curvas.
En el caso de las superficies planas, además, pueden ser paralelas a uno de los 3 planos del triedro u oblicuas a los 3 planos.
Las superficies planas que son paralelas a uno de los planos del triedro tienen la ventaja de que en la perspectiva se ven lo mismo que la proyección en alzado. Además, en las vistas es fácilmente reconocible porque esta superficie se ve en las otras dos vistas como una recta.
En este vídeo puedes encontrar una explicación de cómo realizar la perspectiva isométrica.
¿Qué aplicaciones tiene la Perspectiva Isométrica?
El uso de la Perspectiva Isométrica es amplio. Algunos ejemplos son:
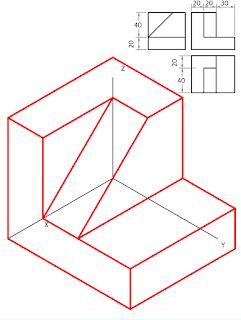
Diseño y dibujo técnico
En el sector del diseño industrial suelen representarse piezas desde varios puntos de vista, perpendiculares a los ejes coordenados naturales. Estos ejes permiten definir una proyección ortogonal. A estas vistas normalmente se les denomina como: planta, elevación y perfil. Siendo planta la vista desde arriba, elevación la vista frontal, y perfil la vista lateral.
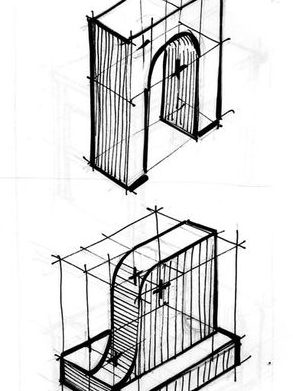
Arquitectura
La proyección isométrica es útil para visualizar de forma sencilla conjuntos de edificios pequeños, produciendo imágenes que recuerdan a fotografías oblicuas tomadas a vista de pájaro, en las cuales la larga distancia entre el observador y el modelo que se representa atenúa el efecto de convergencia de las líneas paralelas propia de la perspectiva de la realidad. También suelen ser habituales los dibujos en sección, que permiten hacerse una idea de la distribución de las habitaciones de una casa de una mejor forma que un simple plano de la distribución en planta.
Videojuegos
En determinados videojuegos es normal encontrarse que se pone en acción a los personajes usando un punto de vista en perspectiva isométrica. Esto permite que se desplacen los elementos gráficos sin modificar el tamaño, limitación que es inevitable para ordenadores con baja capacidad gráfica. La progresiva mejora que se realiza en las capacidades gráficas de los ordenadores ha permitido el uso masivo de sistemas de proyección más realistas, basados en la perspectiva cónica, que es la naturalmente percibida por el ojo humano. En el conjunto existente de proyecciones axonométricas o cilíndricas, existen también otros tipos de perspectivas en función de la posición de los ejes principales, además de por el uso de diferentes coeficientes de reducción para así compensar las distorsiones visuales.
¿Qué es la Perspectiva Axonométrica?
La Perspectiva Axonométrica consiste en un sistema de representación gráfica que se basa en representar elementos geométricos o volúmenes en un plano, mediante la proyección ortogonal, referida a tres ejes ortogonales, de modo que conserven sus proporciones en las tres direcciones espaciales.
Los tres ejes del plano proyectante se tienen que dibujar del siguiente modo:
- El eje que representa la altura suele ser vertical, y los referentes a longitud y ancho pueden disponerse en cualquier ángulo.
- Los ejes del plano guardan entre sí 120º en la perspectiva isométrica, un caso específico de la perspectiva axonométrica. Sin embargo, si los ejes guardan entre sí 90º y 135º pasaría a denominarse perspectiva caballera.
- Con el objetivo de que el dibujo se asemeje más a la realidad, se aplica ocasionalmente un coeficiente de reducción en las medidas paralelas a los ejes de anchura y longitud.
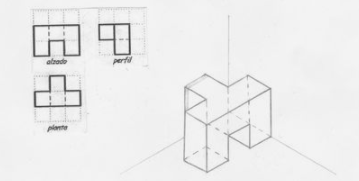
La proyección axonométrica representa la imagen de un cuerpo según se observa desde una dirección oblicua con el fin de revelar información algún lado del mismo. Mientras que el término ortográfica suele estar reservado para las representaciones de objetos donde el eje o plano del objeto es paralelo al plano de proyección.
En la axonometría la escala de los elementos distantes al plano de proyección es similar a la de los elementos cercanos, lo que hace que este tipo de dibujos no se correspondan con la forma en la que se perciben visualmente o aparecen en una fotografía.
Si todavía no te ha quedado claro qué es la perspectiva axonométrica, puedes consultar este vídeo.
¿Qué es la Perspectiva Caballera?
La Perspectiva Caballera consiste en un sistema de representación el cual utiliza la proyección paralela oblicua, y por ello las dimensiones del plano proyectante frontal suelen estar en magnitud verdadera.
Esta perspectiva representa objetos con ciertas deformidades que para algunas personas pueden pasar desapercibidas a simple vista. A la hora de realizar este tipo de perspectiva se toman de referencia los ejes X, Y y Z, se reducen los objetos para poder hacer una representación espacial solo las que están en el eje Y.
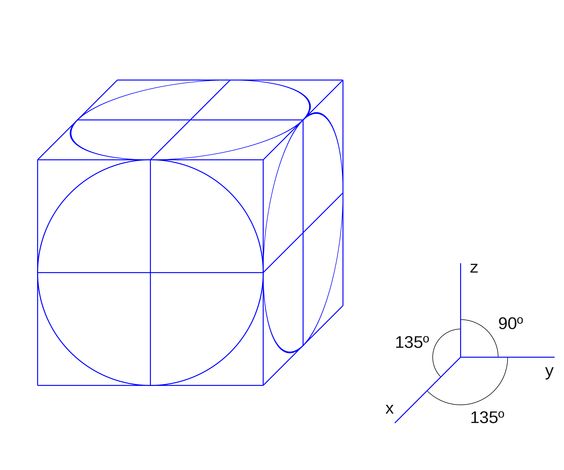
Esta perspectiva se usa cuando es necesario reducir el tamaño de los objetos a representar, aunque usualmente se deforman las características. En la perspectiva caballera, dos de las dimensiones del volumen que se va a representar se proyectan en verdadera magnitud, normalmente son el ancho y el alto, y la tercera, que es la profundidad, se proyecta con un coeficiente de reducción añadido, del cual hablaremos más adelante.
Los ejes Y y Z forman un ángulo de 90°, y el eje X suele tener 45° respecto a los otros. Se suelen adoptar ángulos iguales o múltiplos de 30° y 45°. Se puede dibujar de forma sencilla un volumen a partir de una vista lateral, trazando desde cada vértice líneas paralelas a Y, para reflejar la profundidad del volumen.
Si quieres saber más sobre la perspectiva caballera, te recomendamos el siguiente vídeo.
¿Qué es un Punto de Fuga?
Un punto de fuga en un sistema de proyección, como en este caso puede ser la perspectiva isométrica, se define como el lugar geométrico en el que convergen las proyecciones de las rectas paralelas a una dirección dada en el espacio.
El punto de fuga es considerado un punto impropio, ubicado en el infinito. Un punto de fuga que se corresponde con una determinada dirección en el espacio queda definido por la intersección entre el plano de proyección y un rayo con dicha dirección trazado desde el punto de vista.
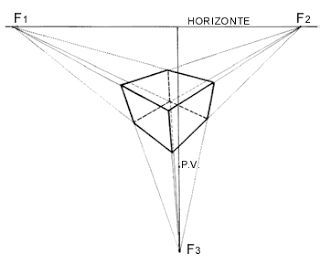
Según las direcciones de los ejes ortogonales respecto al plano de proyección, se pueden distinguir:
- Perspectiva frontal: esta perspectiva contiene un solo punto de fuga y ocurre siempre que una de las caras del cubo es paralela al plano de proyección, por tanto dos ejes del espacio son paralelos a ese plano.
- Perspectiva oblicua: este tipo contiene dos puntos de fuga y ocurre cuando el cubo está de cierta forma ladeado, y solo uno de los ejes espaciales es paralelo al plano de proyección.
- Perspectiva aérea: esta contiene tres puntos de fuga y ocurre cuando el cubo está ladeado y además volcado.
¿Qué es el Coeficiente de Reducción?
A lo largo del artículo se ha mencionado varias veces el coeficiente de reducción. Este coeficiente es una cantidad establecida por la cual deben multiplicarse todas las medidas de un determinado eje para que de esta forma la perspectiva se asemeje a la realidad.
En la perspectiva isométrica todas las medidas de los ejes deben multiplicarse por una misma cantidad, la cual suele ser 0’816, pero para simplificar se puede no utilizar esta cantidad. Si no se utiliza, se dice que el coeficiente utilizado es 1, o lo que es lo mismo, que todas las medidas se multiplican por 1, lo cual equivale a no modificar las medidas.
Puedes encontrar una explicación más detallada en el siguiente vídeo.