Cálculos Tipo para los Muros de Fábricas

De Construmatica

Logonbloc.png Nota: Este artículo ha sido creado gracias a la Normabloc en el marco del Programa de Afiliados de la Construpedia. El contenido está disponible en el sitio web de Normabloc

¡Atención! Esté artículo está sujeto a Derecho de Autor.



Cálculo de comportamiento de placa según EC-6 y CTE SE-F

En el procedimiento de cálculo para muros con acciones laterales del CTE SE-F, se establece un procedimiento de calculo según rotura de placas, el mismo existente ya en el Eurocódigo 6.

Este procedimiento se basa en el prorrateo de los momentos flectores del muro según sus dos direcciones principales marcadas por la alineación o perpendicularidad con los tendeles de la fábrica.

Para este Manual de Normabloc suponemos que los elementos conformantes de la fábrica armada tienen una estructura mas o menos uniforme en cada una de las dos direcciones del tendel, ya que empleando armaduras de tendel prefabricadas en forma de cercha, los materiales van a trabajar en armonía constructiva, es decir no se va a producir, debido al comportamiento individual de cada uno de los componentes, una rotura del comportamiento global.

El método de cálculo que propone el CTE SE-F para muros con acciones laterales es de aplicación también para este tipo de fábrica, puesto que la hipótesis de trabajo sería la misma.

Para facilitar el procedimiento de prorrateo de momentos en la fábrica se ha condensado en una serie de tablas que establecen la distribución de momentos según las dos direcciones determinadas por la configuración básica de toda fábrica tradicional formada por tendeles horizontales y su relación de resistencia y la relación de los lados de la placa, siempre rectangular.

Con estos parámetros establece los coeficientes a aplicar entrando en las formulas:

MSdx1 = μα·qdL2: Rotura paralela a los tendeles.
MSdx2 = α·qdL2: Rotura perpendicular a los tendeles.


Para ver de donde viene todo este procedimiento analicemos más en profundidad una de ellas, por ejemplo el caso de una placa simplemente apoyada en todos sus lados.

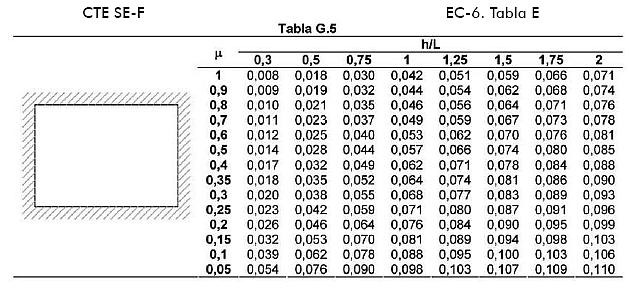
Ejemplificada en la tabla G.5 del actual Código Técnico, antigua E del Eurocódigo 6.

Calc1.png


Los valores que da se pueden derivar del método clásico de líneas de rotura y trabajos virtuales considerando que el material funciona homogéneamente y después este esfuerzo se puede dividir según dos direcciones proporcionalmente a la resistencia de las mismas.

Asi, para el caso de placa apoyada perimetralmente y la que las resistencias son iguales (material isótropo), el razonamiento sería:

h/L = Variable
μ = 1 (linea superior de valores de la tabla)


Según el método de los trabajos virtuales, el trabajo externo para llevar a cabo la rotura es el mismo que el interno a la estructura al realizar las deformaciones.


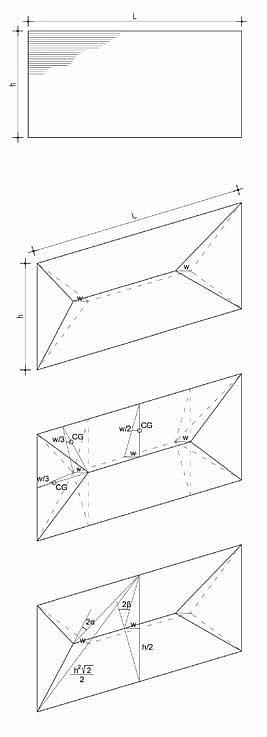
Calc2.png


Para el caso de una placa como la figura, apoyada perimetralmente, el trabajo externo es el necesario para modificar la posición de sus centros de gravedad:

W (trabajo) = Fuerza * movimiento
ΣWext=4*(q*((h*(h/2))/2)*(w/3)) + (q*((L-h)*h)*(w/2))
ΣWext=(q*h2*w)/3)) + (q*(L-h)*h*w)/2


Mientras que el trabajo interno realizado por la placa en su flexión a lo largo de las líneas de rotura es:

ΣWint=4*Mu*(h/(√2))*(2*(w/(h/(√2)))+Mu*(Lh)*2*(w/(h/2))
ΣWint = 8*Mu*w + 4*Mu*w*((L-h)/h)

Donde "Mu" es el momento último necesario para la rotura.


ΣWext = Σwint


Derivamos una formula que nos defina el momento ultimo en función de las dimensiones, "L" y "h" de la placa:

Mu = q*{h2/3 + ((L-h)*h)/2}/{8 + 4*((L-h)/h)]

Donde según la proporción entre las medidas:

L = h >> Mu = 0.0417*q*L2 ~ 0.042 En tabla
L = 2h >> Mu = 0.01735*q*L2 ~ 0.018 En tabla
L = 3h >> Mu = 0.009.25*q*L2 ~ 0.008 (para L = 3.33h)
L >> ∞ >> Mu = 0.125*q*h2


Momento isostático sólo vertical


Téngase en cuenta que el cálculo se realiza para un muro ciego y homogéneo. Cualquier abertura o singularidad en el mismo condicionaría que las líneas de rotura cambiarán y con ellas el sistema de cálculo por lo que las tablas serían de utilidad nula en el nuevo caso.

Siguiendo este razonamiento se podrían derivar todos los coeficientes que aparecen en las sucesivas tablas del EC-6 y CTE SE-F.

Este tipo de cálculo no se puede utilizar para muros conformados con armado tradicional o con costillas, siendo el comportamiento de estos mas parecido al análisis de estructuras emparrilladas de vigas.

Una forma de analizar estas fábricas consiste en analizar los distintos elementos, zunchos o costillas, con respecto a sus esfuerzos como si estos elementos fueran los únicos elementos resistentes del paño.

Ejemplo de Cálculo con el Sistema de Albañilería Integral: SAI

Así, un ejemplo sería el cálculo de una partición de 6,00m de altura con costillas cada 3,50m ante una carga de 0.2 kN/m2:

Características geométricas

  • Paño con sujeción en cabeza.
  • Tipo de bloque: BHH 39x19x19cm
  • Altura libre entre forjados: H=6,00m.
  • Distancia entre costillas: L=3,50m.
  • Espesor eficaz: tef=190mm.
  • Armado horizontal: Murfor RND.4/Z-150mm cada 60cm
  • Costillas verticales AllWall: AW-COS.10/-140mm

Comprobación de la fábrica

  • Resistencia a flexión horizontal de la fábrica con armadura:
(armadura de tendel: RND.4/Z-150Φ4mm/60cm; As=21mm2/m; Z=150mm)
Mux2=AsfydZ=1,366kNm/m
  • Comprobación a momento (flexión horizontal): Mdx2 < Mux2
(para una carga lateral w=0,2kN/m2; y una luz de flexión de L=3,50m)
Mdx2=γfwL2/12=0,306kNm/m < 1,366kNm/m; CUMPLE.
  • Comprobación de costillas (cordones 1Φ10; Z=140mm; diagonal 1Φ5):
  • Momento máximo de cálculo a flexión vertical en costillas:
(biapoyada; H=6,00m; separación entre costillas L=3,50m)
Mdx1, costilla= γfwLH2/8=4,73kNm
  • Cortante máximo de cálculo a flexión vertical en costillas:
Vdx1, costilla= γfwLH/2=3.15kN
  • Comprobación de resistencia a momento flector: Mux1 > Mdx1
Mux1, costilla=As, cordonesfydZ=4,78kNm > 4,73kNm; CUMPLE.
Vu, costilla=As, celosíafydcosα=6,95kN > 3,15kN; CUMPLE.

Artículos Relacionados

Obtenido de «https://www.construmatica.com/construpedia/index.php?title=Cálculos_Tipo_para_los_Muros_de_Fábricas&oldid=13618»