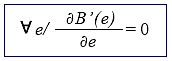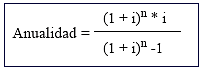Modelo de Cálculo para el Aislamiento Óptimo

	Nota: Este artículo ha sido creado gracias a la AFELMA en el marco del Programa de Afiliados de la Construpedia. El contenido está disponible en el sitio web de AFELMA ¡Atención! Esté artículo está sujeto a Derechos de Autor.

El contenido de este artículo puede estar desactualizado

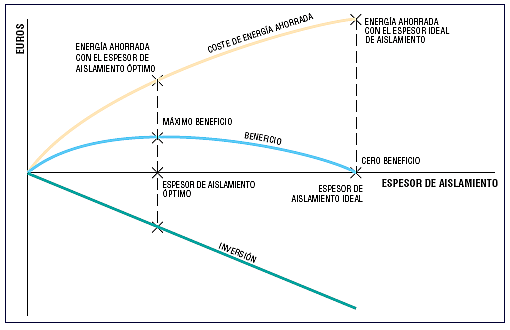
Con el objetivo de encontrar el aislamiento óptimo, se ha usado un análisis de coste-beneficio. Este modelo de cálculo es similar al usado en el informe de ECOFYS: "Cost-Effective Climate Protection in the EU building stock":

Para realizar esto, se creó una función "beneficio económico" (B (e)) definida como la diferencia entre "ingresos" (I (e)) (costes anuales totales derivados del ahorro cuando se aumenta el aislamiento) y "gastos" (G (e)) (Coste anual de la inversión al aumentar el aislamiento).

Esto es:

Para obtener el máximo de la función, esto es, el máximo del "Beneficio económico", se debe derivar la función resultado e igualarla a cero (para verificar que B(e) es el máximo de la función, debe chequearse que la segunda derivada es menos que cero).

B (e) es máximo:

Siendo "e" el aumento óptimo del grosor resultando el máximo beneficio.

En nuestro caso, el "Ingreso" se expresa mediante la siguiente fórmula:

Siendo:

ΔΣ: Aumento de la energía ahorrada como resultado del aumento en "e" cm del grosor del aislamiento sobre el mínimo necesario para satisfacer los requerimientos establecidos por el CTE para el valor de U.

P_energía: Precio medio de la energía durante el tiempo equivalente a la vida del aislamiento.

Y los "Gastos" vienen expresados en la siguiente fórmula:

Ct_aislamiento = Coste Aislamiento + Gastos generales + Beneficio industrial + Impuestos

Anualidad se expresa como:

i = Ratio de interés

n = Vida del aislamiento

Fc = Factor de conversión.

Ideal y óptimo espesor de aislamiento

Modelo de Cálculo para el Aislamiento Óptimo

De Construmatica

Artículos Relacionados