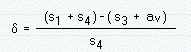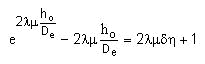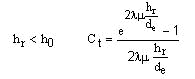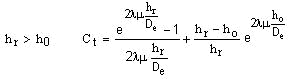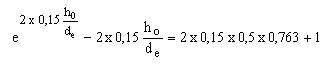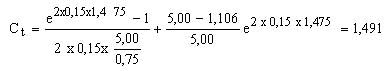Tuberías de Hormigón: Instalación en Terraplén

	Nota: Este artículo ha sido creado gracias a ATHA en el marco del Programa de Afiliados de la Construpedia. El contenido pertenece a la publicación Manual de Diseño y Cálculo para la Fabricación de Tuberías de Hormigón Armado, disponible en el sitio web . ¡Atención! Esté artículo está sujeto a Derecho de Autor.

Exposición

En los casos en que la generatriz superior del tubo tenga que quedar por encima del terreno natural es necesario terraplenar hasta alcanzar la cota final prevista. En estas condiciones, la base de la conducción puede situarse por debajo del terreno natural, lo que obliga a abrir una zanja más o menos profunda.

Cuando la conducción sobresale de dicha zanja, diremos que su proyección es positiva y la instalación es en terraplén.

Cuando la conducción se encuentra totalmente en el interior de la zanja, diremos que su proyección es negativa y se tratará de una instalación en zanja terraplenada.

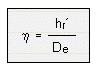
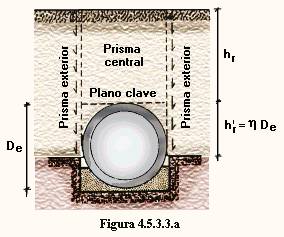
Se llama "razón de proyección" positiva h, al cociente de dividir la altura h_r ' del relleno de terraplén, medida desde la base de éste hasta el plano de clave ( figura 4.5.3.a), por la dimensión De del diámetro exterior de la conducción.

Si la anchura de zanja es superior a la de transición, se toma h = 1,0.

Consideremos el prisma de tierras situado sobre el plano de clave, entre los dos planos verticales tangentes a la superficie exterior de la conducción; este prisma, situado directamente sobre la conducción, cuya anchura es De y cuya longitud tomaremos igual a 1 metro, recibe el nombre de "prisma central" (figura 4.5.3.3.a). Llamaremos "prismas exteriores" a los constituidos por el relleno situado a ambos lados del prisma central y que se apoya en el terreno natural.

En condiciones de proyección positiva, la altura hr del relleno que forma el prisma central será menor que la altura hr + hr ' del relleno situado en los prismas exteriores.

h_r < h_r + h_r ´ = h_r + h D_e

En consecuencia, el relleno de los prismas exteriores asentará más que el del prisma central, siendo la diferencia de asientos el asiento correspondiente a la altura h_r' = h De. El rozamiento entre los prismas exteriores y el central hará que, si no existieran otras deformaciones, aquellos "tiren" hacia debajo de éste, con lo que la conducción recibirá una carga superior al peso del prisma central, es decir, lo contrario de lo que ocurría en la instalación en zanja.

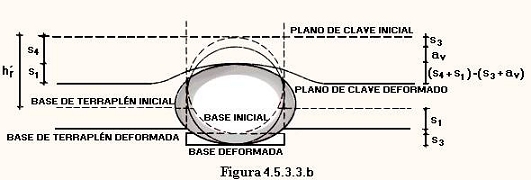
Sin embargo, es necesario considerar otras deformaciones, además de la producida por dicha diferencia de asientos. En conjunto, estas deformaciones, son (figura 4.5.3.3.b):

s₁ = deformación de la base en que se apoyan los prismas exteriores

s₃ = deformación de la base de la conducción

a_v = deformación vertical de la propia conducción

s₄ = deformación correspondiente a la altura de relleno hr '

Los puntos pertenecientes al plano de clave habrán experimentado descensos, que para el prisma central presentan un valor mínimo s₃ + a_v , y para los prismas exteriores un valor máximo de s₁ + s₄ . El deslizamiento entre prismas, que originan las fuerzas de rozamiento que se oponen a él, tienen un valor

(s₁ + s₄ ) - ( s₃ + a_v )

el cual dividido por s₄ nos da la "razón de asentamiento" d

Para d = 0, la carga de relleno qr que soporta la conducción es igual al peso de las tierras contenidas en el prisma central, al ser nulo el deslizamiento y no aparecer, por tanto, fuerzas de rozamiento.

Cuando el terreno natural sobre el que descansan el terraplén y la conducción es muy rígido, es decir, con un módulo de deformación longitudinal relativamente grande (por ejemplo roca), y además la tubería es prácticamente indeformable, pueden considerarse s₁ = s₃ = a_v = 0 y resulta d = 1, razón de asentamiento para la que puede considerarse que la carga qr ha alcanzado su máximo valor para una razón de proyección dada, aunque puedan considerarse casos en que d > 1.

Cuando ( s₃ + a_v ) > ( s₁ + s₄ ), la razón de asentamiento se hace negativa; entonces el prisma central desciende más que los exteriores y las fuerzas de rozamiento invierten su sentido con lo que q_r se hace menor que el peso del prisma central. Diremos que se trata de una instalación en terraplén en "condición de zanja inducida". Esto puede producirse cuando la base en la que descansa el terraplén y la conducción es muy compresible, por ejemplo cuando esta base se ha formado por terraplenado. En estas condiciones, al ir compactando, a medida que las tierras se elevan a ambos lados de la conducción, la base de los prismas exteriores queda más compactada que la base de la tubería, con lo que ésta sufrirá mayores asientos ( s₃ > s₁ ). Si además los tubos son muy deformables ( a_v relativamente grande) es fácil que resulte d < 0. Una razón de proyección pequeña ( h_r' y s₄ pequeños) colabora a este resultado. En estos casos, tomando d > 0 se estará del lado de la seguridad.

La determinación de la razón de asentamiento exige calcular las deformaciones s₁ y s₃ conociendo la presión que sufren las bases bajo el peso de las tierras, así como su módulo de deformación longitudinal; la deformación s₄ , teniendo en cuenta la compactación; y la deformación a_v de la tubería bajo las acciones verticales y horizontales que la solicitan.

No siendo fácil llegar a conocer con precisión el valor de d, se acostumbra a adoptar los siguientes:

Base rígida (roca o suelo muy compacto)

d = 1,0

Base de suelo natural ordinario

d = 0,5

Base muy asentable (terraplén no bien compactado, etc.)

d = 0,3

En caso de duda, un valor superior de d sitúa del lado de la seguridad.

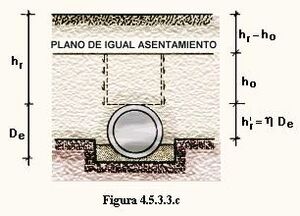
A medida que el terraplén se eleva sobre el plano de clave, las diferencias de asiento entre el prisma central y los exteriores se van haciendo menores, hasta alcanzar un nivel para el que se igualan. El plano horizontal considerado a este nivel se denomina "plano de igual asentamiento", y su distancia al de clave "altura de igual asentamiento", h_o .

Por encima del plano de igual asentamiento no existen deslizamientos entre el prisma central y los exteriores, ni por tanto fuerzas de rozamiento. Las tierras sobre él pueden considerarse como una sobrecarga uniforme sobre dicho plano, correspondiente al peso de relleno con una altura h_r - h_o (figura 4.5.3.3.c).

El valor de ho puede obtenerse de la ecuación

Fijados los valores de l, m, d, h , el segundo miembro es una constante. Basta entonces dar valores a h_o/D_e hasta encontrar el que verifica la igualdad, lo que se consigue rápidamente.

Por ejemplo, para l m = 0,15 y h = 0,763 se obtienen los siguientes valores de h_o / D_e para los valores de d antes indicados.

Tabla 4.5.3.3

Multiplicando el valor de h_o / D_e obtenido por el diámetro exterior D_e de la conducción, hallamos la altura de igual asentamiento h_o .

Cuando hr < ho, las fuerzas de rozamiento llegan hasta la superficie del terraplén ( figura 4.5.3.3.a). En estas condiciones, por un razonamiento análogo al visto para el caso de instalación en zanja, la carga que el relleno produce sobre la conducción, resulta

q_r = C_t g_r h_r D_e

con q_r en kN/m, g_r en kN/m³ y, h_r y D_e en m.

En dicha expresión, el coeficiente de Marston para terraplén, C_t , tiene el valor

Cuando h_r > h_o , es necesario añadir a la carga sobre la conducción producida por el relleno hasta la altura h la correspondiente a la sobrecarga de relleno con altura h_o-h_r. Esta última carga se calcula mediante una expresión semejante a la obtenida en el caso de instalación en zanja.

La carga qr producida sobre la conducción por la altura de relleno h_rse obtiene por la misma expresión dada anteriormente.

q_r = C_t g_r h_r D_e

Pero tomando ahora como coeficiente de Marston

Ejemplo

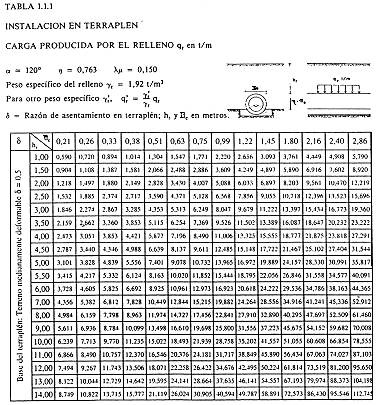
Supongamos el mismo tubo considerado en el apartado anterior, instalado ahora en terraplén con los siguientes datos: D = 60 cm; D_e = 75 cm; h_r = 5,0 cm; g_r = 1,92 t/m³; l m = 0,150; h = 0,763. El terreno natural sobre el que se apoya la conducción y que sirve de base al relleno, es un suelo ordinario, ni muy rígido ni muy deformable, por lo que se toma como razón de asentamiento d = 0,5.

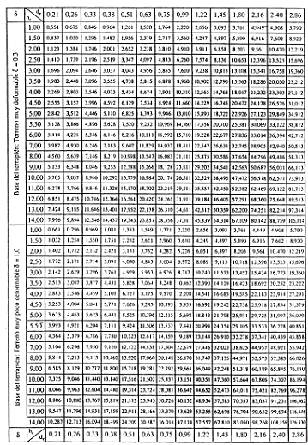
Acudiendo a la tabla III, se obtiene directamente q_r = 107,32 kN/m.

Veamos cómo se ha calculado este valor:

La altura ho del plano de igual asentamiento, se obtiene resolviendo

se verifica para h_o /D_e = 1,475, es decir h_o = 1,475 x 0,75 = 1,106m < h_r

q_r = 1,491 x 19,2 x 5,00 x 0,75 = 107,32 kN/m

Puede observarse que este valor de q_r ( q_r = 107,32 kN/m ) es muy superior al obtenido en el ejemplo del apartado 4.5.3.2, cuando el tubo se encontraba instalado en una zanja de anchura b = 1,20 m ( qrz = 65,76 kN/m ).

Si en este caso fuéramos aumentando b, manteniendo h_r = 5,00 m, el valor qr iría aumentando (véase la tabla III) hasta igualar al de qrt para una anchura comprendida entre b= 1,60m y b=1,70m; la anchura correspondiente sería la de transición. Para b = 1,70m, la carga sobre el tubo instalado en zanja será q_r = q_rt = 107,32 kN/m, y no 108,42 kN/m como se lee en la tabla II.

Enlaces externos

Tuberías de Hormigón: Instalación en Terraplén

De Construmatica

Artículos Relacionados

Enlaces externos