Encargado de Obra - Interpretación de Planos: Cálculo de una Escala
De Construmatica
| Nota: Este artículo ha sido creado gracias a la Fundación Laboral de la Construcción en el marco del Programa de Afiliados de la Construpedia. El contenido pertenece a la publicación Encargado de obra. Parte común. Interpretación de planos disponible en el sitio web Fundación Laboral de la Construcción
¡Atención! Esté artículo está sujeto a Derecho de Autor. © Fundación Laboral de la Construcción. |
|---|
Cálculo de una escala
Sucede en ocasiones que cuando cierta documentación gráfica llega a nuestras manos ha sufrido alteraciones de tamaño no deseables fruto de un proceso continuado de reproducción.
Cuando esto sucede, a menudo el valor numérico de la escala que figura en su rotulación no se corresponde con la realidad del dibujo, por lo que conviene hallar la escala verdadera a la que corresponde realmente la documentación.
Con el fin de hallar la escala real del dibujo, tomaremos una cota, es decir, un segmento cuyo valor real conozcamos, bien porque nos venga dado, bien porque sepamos de antemano su medida real.
A esta cota o medida real, siempre expresada en unidades del sistema métrico, la llamaremos "medida del objeto en la realidad", en adelante MOR.
Debemos entonces medir con una regla sobre dicho segmento representado sobre el papel sin olvidar que conocemos su medida real.
A la resultante de dicha medición la llamaremos "medida del objeto en el dibujo", en adelante MOD.
Escala = MOD/MOR
El cálculo de una escala se realiza mediante la reducción del cociente entre la medida de un segmento sobre el papel (MOD) y el valor de dicho segmento en la realidad (MOR). La representación numérica de dicha escala se considera adecuada cuando el numerador queda reducido a la unidad, para lo cual se reducirán los valores obtenidos a común denominador, simplificando los comunes.
Ambos valores deberán estar en las mismas unidades de medida para poder ser simplificados.
Con el fin de afianzar este conocimiento, realizaremos un caso práctico de cálculo de escala.
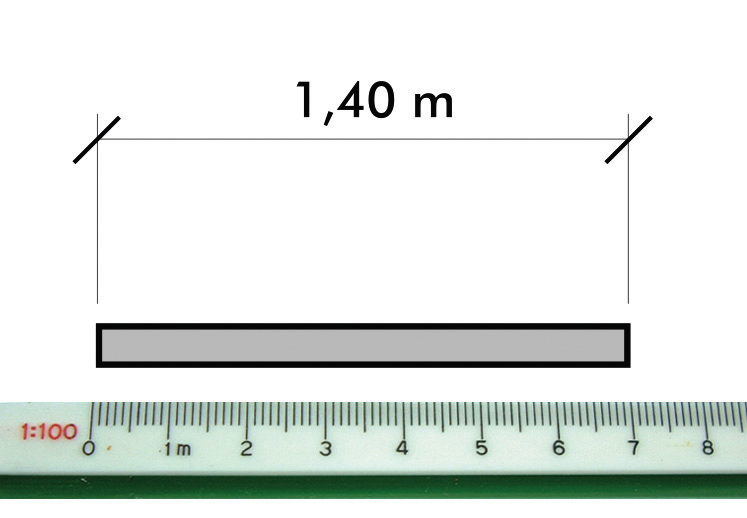
Ejemplo: Un segmento en la realidad mide 1,40 m y así aparece acotado. Al medir con la regla sobre el dibujo, contabilizamos 7 cm.
¿Qué escala se ha aplicado?
Solución:
Aplicamos la fórmula:
Escala = MOD/MOR = 7cm/1,40m = 7cm/140m
Reduciendo a común denominador,
Escala = 1.7/1.2.2.5.7 ; simplificando los comunes: Escala = 1/20
Es fundamental que al hallar la escala numérica el resultado obtenido quede en forma de quebrado de tal forma que el numerador sea la unidad y el denominador un número entero.
Una forma sencilla de obtener esto sin recurrir a la reducción a común denominador consiste en dividir la cifra obtenida en el denominador (MOR) por la cifra del numerador (MOD).
El resultado obtenido será el denominador de la escala, siendo el numerador siempre 1.
Ejemplo: De una forma más sencilla, obtendremos el valor del denominador de la escala sin más que dividir 140 entre 7. El resultado es 20. Ese será el valor del denominador de la escala siendo el numerador siempre 1.
140/7=20; Escala = 1/20
En caso de no resultar un número entero, no hay que dudar en redondear al alza o a la baja tratando de buscar el número más cercano a cualquiera de las escalas normalizadas que existen o, en su defecto, a las que aparecen en los utensilios de medición.
Artículos Relacionados
- Interpretación de Planos: Introducción
- Interpretación de Planos: Mapa Conceptual
- Interpretación de Planos: Concepto de Escala, Proporcionalidad, Razón o Proporción
- Interpretación de Planos: Escala Numérica y Escala Gráfica
- Interpretación de Planos: Escalas Normalizadas
- Interpretación de Planos: Útiles Adecuados para el Trabajo con Escalas
- Interpretación de Planos: Resumen
- Interpretación de Planos: Terminología