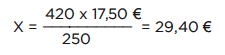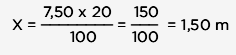Formación en Oficios de la Construcción. Solados y Alicatados: Referentes Matemáticos
De Construmatica
| Nota: Este artículo ha sido creado gracias a la Fundación Laboral de la Construcción en el marco del Programa de Afiliados de la Construpedia. El contenido pertenece a la publicación Solados y alicatados disponible en el sitio web Fundación Laboral de la Construcción
¡Atención! Esté artículo está sujeto a Derecho de Autor. © Fundación Laboral de la Construcción. |
|---|
Referentes matemáticos
Para realizar cualquier trabajo en construcción siempre tenemos la limitación que nos imponen las dimensiones del local, de la vivienda o del solar. Así, cada elemento constructivo que utilicemos, desde un sencillo ladrillo hasta un edificio completo tienen unas medidas exactas.
Por lo tanto las operaciones matemáticas: suma (+), resta (-), multiplicación (x) o división (/ ó :), se utilizan continuamente y debemos alcanzar cierta destreza en dichas operaciones.
Manejamos tanto números enteros (28, 10, 12,...) como decimales (3,50; 20,22; 46,15;...) y fracciones (1/2, 3/4, 5/6,...).
Conviene que recordemos algunas de las operaciones de uso más habitual y que tienen muchas aplicaciones.
Operaciones de un cantidad por la unidad seguida de ceros
a. Multiplicación
Para multiplicar una cantidad por la unidad seguida de ceros, se añaden a la cantidad tantos ceros como acompañan a la unidad y si el número es decimal, se desplaza la coma hacia a la derecha tantos lugares como ceros acompañan a la unidad; si es necesario se añaden ceros.
b. División
Se opera de forma inversa que en la multiplicación. Para dividir una cantidad por la unidad seguida de ceros, se desplaza la coma hacia la izquierda tantos lugares como ceros acompañan a la unidad, si es necesario se añaden ceros por delante de la cantidad.
Para multiplicar se corre la coma hacia la derecha.
Ejemplos:
3,0 x 1.000 = 3.000,0
3,5 x 10 = 35,0
42,27 x 100 = 4.227,0
Para dividir se corre la coma hacia la izquierda.
Ejemplos:
3 : 1.000 = 0,003
356 : 10 = 35,60
35,6 : 100 = 0,356
Operaciones con unidades
En longitud, la unidad básica es el metro (m), en superficie es el metro cuadrado (m2) y en volumen es el metro cúbico (m3).
Para poder realizar operaciones matemáticas (+, -, x, :) hay que igualar las unidades. Es decir nunca podemos operar metros (m) con centímetros (cm).
Las equivalencias entre las unidades más utilizadas son las siguientes:
a. Medidas de longitud
1 km (kilómetro) = 1.000 m (metros)
1 dm (decímetro) = 0,10 m
1 cm (centímetro) = 0,01 m
1 mm (milímetro ) = 0,001 m
b. Medidas de superficie
1 km2 (kilómetro cuadrado) = 1.000.000 m2 (metros cuadrados)
1 dm2 (decímetro cuadrado) = 0,01 m2
1 cm2 (centímetro cuadrado) = 0,0001 m2
1 mm2 (milímetro cuadrado) = 0,000001 m2
Ejemplo:
¿Cuántos ladrillos de 25 cm de largo hay en una hilada de un muro que tiene 2,75 m de longitud? (Se prescinde del grueso de la junta entre los ladrillos).
Los metros hay que pasarlos a centímetros: 2,75 m = 275 cm
Dividimos esta longitud entre la dimensión de cada ladrillo:
275 : 25 = 11 ladrillos.
La regla de tres
Cuando tenemos dos magnitudes que se relacionan entre sí, por ejemplo ladrillos y pesetas, y se conocen dos valores de una magnitud y uno solo de la otra, si queremos hallar el cuarto, la "Regla de tres" es el procedimiento para encontrar su valor.
Así tenemos el caso siguiente:
Ejemplo:
250 ladrillos nos han costado 17,50 €. ¿Cuánto nos costarán 420 ladrillos?
Se siguen los siguientes pasos:
250 ladrs. _________ 17,50 €.
420 ladrs. _________ X €.
Se trata de una proporción en la que se desconoce un término:
Para resolverlo se multiplican en cruz los dos términos conocidos y dividimos por el otro:
Un caso especial de la "Regla de tres" es el "Tanto por ciento" (%), de aplicación directa, tanto en la vida cotidiana como en nuestra profesión.
El "Tanto por ciento" se utiliza en construcción para: calcular la pendiente de un pavimento con inclinación que sirve para verter en un saneamiento, para la inclinación de las conducciones, para calcular la pendiente de las cubiertas, etc.
Ejemplo:
Vamos a ilustrar este cálculo con un ejemplo:
Tenemos el caso de una cubierta de teja de 7,50 m de longitud. Debe tener una pendiente del 20%. (quiere decir que por cada 100 m. sube 20 m.). ¿Cómo sabemos su punto más alto?.
Aplicamos el "tanto por ciento" (Regla de tres):
100 m _________ 20 m
7,50 m _________ X
El punto más alto de la cubierta está a 1,50 m.