Oficios. Prefabricados de Placas de Yeso Laminado: Referentes Geométricos
De Construmatica
| Nota: Este artículo ha sido creado gracias a la Fundación Laboral de la Construcción en el marco del Programa de Afiliados de la Construpedia. El contenido pertenece a la publicación Encargado de Obra: Calidad y Medio Ambiente disponible en el sitio web Fundación Laboral de la Construcción
¡Atención! Esté artículo está sujeto a Derecho de Autor. © Fundación Laboral de la Construcción. |
|---|
Referentes geométricos
La geometría es la parte de las matemáticas que trata de las propiedades de las figuras, tanto en el plano como en el espacio.
En nuestra actividad es muy frecuente el uso de la geometría en las aplicaciones siguientes:
- - Cálculo de superficies.
- - Cálculo de volúmenes.
- - Replanteos.
Cálculo de superficies
Recordemos el concepto de algunas figuras geométricas y cómo realizar el cálculo de sus superficies.
- - Triángulo. Es un polígono cerrado formado por tres rectas y la suma de sus ángulos es 180º.
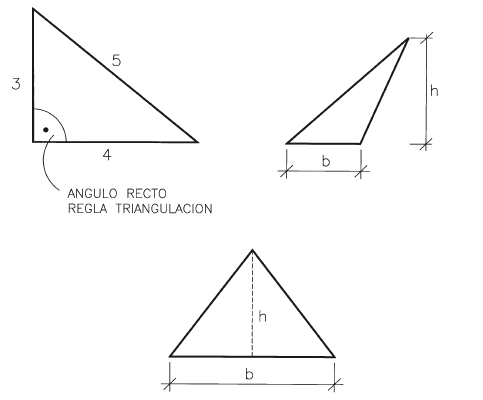
Cuando uno de los ángulos de un triángulo tiene 90º, es decir, es recto y por lo tanto los tanto los lados adyacentes son perpendiculares, el triángulo se denomina rectángulo.
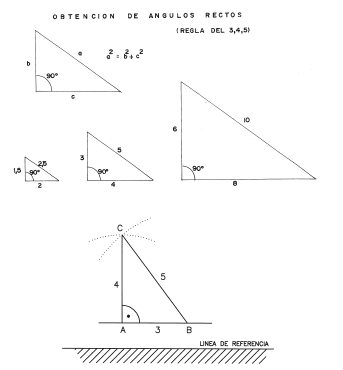
Todos los triángulos rectángulos cumplen el Teorema de Pitágoras: a2 = c2 + b2
La aplicación de este teorema nos servirá para la comprobación del ángulo recto.
Para hallar el área o superficie de un triángulo se emplea la siguiente fórmula (figura 3):
Para comprobar la ortogonalidad (dos rectas son ortogonales cuando forman un ángulo recto, es decir que tiene 900), nos ayudamos de la escuadra (herramienta del albañil) o con la llamada Regla 3, 4 y 5.
Ésta consiste en utilizar una cinta métrica o una cuerda en la que se han marcado las siguientes dimensiones: 3, 4 y 5 (éstas pueden ser en cm, en m o múltiplos de 3, 4 ó 5).
Su empleo se basa en la propiedad del triángulo rectángulo. Si tomamos como referencia (figura 2) una pared y trazamos una paralela a ella AB y que mide 3. Tomando origen en B y en A, con las medidas 5 y 4, respectivamente trazamos dos arcos en circunferencia, que se cortan en el punto C. La recta AC, que mide 4, es perpendicular a AB. Por tanto, el triángulo ABC es rectángulo. Los lados del triángulo son proporcionales a las dimensiones 3, 4 y 5.
Para comprobar que dos rectas son ortogonales podemos utilizar dos cintas métricas con sus orígenes situados a una distancia de 3 m sobre una de las líneas. Si al extender las dos cintas hasta 4 y 5 m respectivamente, hacemos coincidir estos valores, el punto de unión deberá estar situado sobre la línea perpendicular.
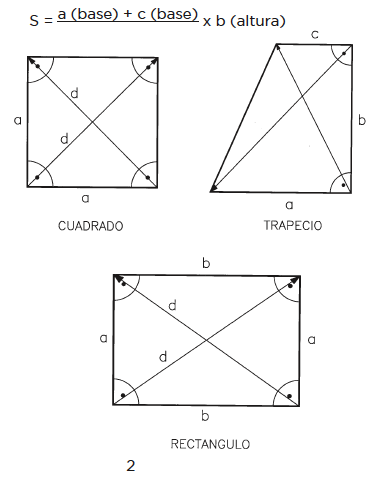
- - Cuadrado. Es una figura plana cerrada por cuatro rectas iguales que forman cuatro ángulos rectos. También son iguales las diagonales (diagonal es la recta que une dos vértices opuestos).
Para hallar su superficie se aplica la siguiente fórmula (figura 4):
S = a (lado) x a (lado) = a2
- - Rectángulo. Es un polígono cerrado formado por cuatro rectas iguales dos a dos y sus ángulos son rectos. Sus diagonales son también iguales.
La superficie del rectángulo se calcula como en el caso anterior:
S = a (lado) x b (lado)
- - Trapecio. Es una figura irregular que tiene paralelos dos de sus lados, los cuales se llaman bases; los otros dos lados unen las citadas bases.
Para conocer su área, aplicamos la siguiente fórmula:
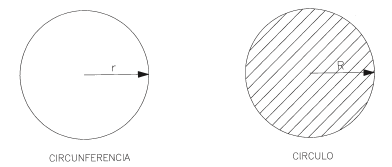
- - Circunferencia. Es una curva plana y cerrada, en la que todos sus puntos equidistan del centro.
La longitud de la circunferencia está en función del radio (r) y de un número constante, llamado número π (π = 3,14)
L = 2 x π x r
- Círculo. Es la superficie plana contenida dentro de una circunferencia.
Su superficie, como en el caso anterior, está en función de π y del radio (r).
S = π x r2
Cualquier superficie, aunque tenga una forma irregular, siempre se puede descomponer en figuras geométricas más sencillas y regulares.
Observamos que un rectángulo se puede descomponer en dos triángulos rectángulos. A un trapecio se le puede considerar formado por un rectángulo y uno o dos triángulos rectángulos, dependiendo del tipo de trapecio.
Toda superficie, aunque tenga forma irregular, se puede descomponer en figuras geométricas sencillas (triángulos o rectángulos) y calcularse como la suma de éstas.
Cálculo de volúmenes
El volumen es otro de los temas que tienen una aplicación muy habitual en nuestra profesión. Todos los elementos constructivos ocupan un volumen y muchas veces es necesario realizar los cálculos oportunos.
Como en el caso de las superficies, hay muchas figuras geométricas regulares que tienen una fórmula de aplicación sencilla: la esfera, el cubo, el prisma, la pirámide, el cilindro y el cono.
Ejemplo: Para ilustrar este concepto, vamos a realizar un cálculo muy sencillo del volumen de un muro con las siguientes dimensiones: 32 m de largo; 2,70 m de alto y 15 cm de espesor.