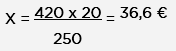Oficios. Prefabricados de Placas de Yeso Laminado: Referentes Matemáticos
De Construmatica
| Nota: Este artículo ha sido creado gracias a la Fundación Laboral de la Construcción en el marco del Programa de Afiliados de la Construpedia. El contenido pertenece a la publicación Encargado de Obra: Calidad y Medio Ambiente disponible en el sitio web Fundación Laboral de la Construcción
¡Atención! Esté artículo está sujeto a Derecho de Autor. © Fundación Laboral de la Construcción. |
|---|
Referentes matemáticos
Para realizar cualquier trabajo en construcción siempre tenemos la limitación que nos imponen las dimensiones del local, de la vivienda o del solar. Así, cada elemento constructivo que utilicemos, desde un sencillo ladrillo hasta un edificio completo tienen unas medidas exactas.
Por lo tanto las operaciones matemáticas: suma (+), resta (-), multiplicación (x) o división (/ ó :), se utilizan continuamente y debemos alcanzar cierta destreza en dichas operaciones.
Manejamos tanto números enteros (28, 10, 12,...) como decimales
(3,50; 20,22; 46,15;...) y fracciones (1/2, 3/4, 5/6,...).
Conviene que recordemos algunas de las operaciones de uso más habitual y que tienen muchas aplicaciones.
Operaciones de una cantidad por la unidad seguida de ceros.
Multiplicación:
Para multiplicar una cantidad por la unidad seguida de ceros, se añaden a la cantidad tantos ceros como acompañan a la unidad y si el número es decimal, se desplaza la coma hacia a la derecha tantos lugares como ceros acompañan a la unidad; si es necesario se añaden ceros.
División:
Se opera de forma inversa que en la multiplicación. Para dividir una cantidad por la unidad seguida de ceros, se desplaza la coma hacia la izquierda tantos lugares como ceros acompañan a la unidad, si es necesario se añaden ceros por delante de la cantidad.
Recordar: para multiplicar se desplaza la coma hacia la derecha.
Ejemplos:
3,0 x 1.000 = 3.000,0
3,5 x 10 = 35,0
42,27 x 100 = 4.227,0
Recordar: para dividir se desplaza la coma hacia la izquierda.
Ejemplos:
3 : 1.000 = 0,003
356 : 10 = 35,60
35,6 : 100 = 0,356
Operaciones con unidades
En longitud, la unidad básica es el metro (m), en superficie es el metro cuadrado (m2) y en volumen es el metro cúbico (m3).
Para poder realizar operaciones matemáticas (+, -, x, :) hay que igualar las unidades. Es decir, nunca podemos operar metros (m) con centímetros (cm).
Las equivalencias entre las unidades más utilizadas son las siguientes:
Medidas de longitud:
1 km (kilómetro) = 1.000 m (metros)
1 dm (decímetro) = 0,10 m
1 cm (centímetro) = 0,01 m
1 mm (milímetro ) = 0,001 m
Medidas de superficie:
1 km2 (kilómetro cuadrado) = 1.000.000 m2 (metros cuadrados)
1 dm2 (decímetro cuadrado) = 0,01 m2
1 cm2 (centímetro cuadrado) = 0,0001 m2
1 mm2 (milímetro cuadrado) = 0,000001 m2
La Regla de tres
Cuando tenemos dos magnitudes que se relacionan entre sí, por ejemplo ladrillos y pesetas, y se conocen dos valores de una magnitud y uno solo de la otra, si queremos hallar el cuarto, la "Regla de tres" es el procedimiento para encontrar su valor.
Ejemplo: Así tenemos el caso siguiente:
250 ladrillos nos han costado 20 €. ¿Cuánto nos costarán 420 ladrillos?.
Se siguen los siguientes pasos:
250 ladrs. —————— 20 €
420 ladrs. —————— X €
Se trata de una proporción en la que se desconoce un término:
Para resolverlo se multiplican en cruz los dos términos conocidos y dividimos por el otro:
Un caso especial de la "Regla de tres" es el "Tanto por ciento" (%), de aplicación directa, tanto en la vida cotidiana como en nuestra profesión.
El "Tanto por ciento" se utiliza en construcción para: calcular la pendiente de un pavimento con inclinación que sirve para verter en un saneamiento, para la inclinación de las conducciones, para calcular la pendiente de las cubiertas, etc.
Ejemplo: Vamos a ilustrar este cálculo con un ejemplo:
Tenemos el caso de una cubierta de teja de 7,50 m de longitud. Debe tener una pendiente del 20%. (quiere decir que por cada 100 m sube 20 m). ¿Cómo sabemos su punto más alto?. Aplicamos el "tanto por ciento" (Regla de tres):
100 m ————— 20 m
7,50 m ————— X
El punto más alto de la cubierta está a 1,50 m